Целый ряд исследователей в разных странах предпринимал попытки раскрыть механизм λ-перехода в кристаллах ферроцена.
Изучение дифракции электронов в газовой фазе при 673К показало наличие свободного внутреннего вращения С5H5-колец ферроцена. Более позднее исследование дифракции электронов при 413К обнаружило равновесие между молекулами со свободным вращением и молекулами в заслоненной (призматической) конформации (симметрия C5h) с барьером внутреннего вращения около 4,2 кДж·моль-1. Напротив, изучение дифракции нейтронов на кристаллах ферроцена при комнатной температуре показало наличие неупорядоченности, вызванной существованием смеси (в соотношении 2:1) двух различных ориентации молекул в заторможенной конформации, получающихся одна из другой при вращении молекулы как целого на 36° вокруг оси симметрии C5d молекулы.
Однако, отмечено, что экспериментальные результаты согласуются и с моделью кристалла, состоящего из смеси одной трети молекул в заторможенной – и двух третей молекул в заслоненной конформации.
Изучена температурная зависимость интенсивности двух полос в ИК-спектре ферроцена, относящихся к колебаниям по связи Fe-C5H5 в области температур фазового перехода. Понижение температуры приводит к появлению и затем увеличению интенсивности этих колебаний, хотя собственно в точке фазового перехода нет резкого изменения интенсивности. Полученные результаты показывают, что при низких температурах существует упорядоченная решетка с нецентросимметричной ячейкой. Высокотемпературная же фаза представляет собой центросимметричную решетку, содержащую преобладающее число заторможенных молекул (симметрия D5d).
На основании рентгеноструктурных исследований в области 80-295К сделан вывод о том, что при температуре 164К кристаллы ферроцена переходят из триклинной в неупорядоченную моноклинную модификацию.
С целью проверки возможности использования метода ДСК для изучения фазовых переходов в кристаллах металлоорганических соединений, изучили кривую теплоемкости ферроцена в интервале 120-230К. Величины теплоемкости (за исключением области максимума Сp) в пределах ошибки эксперимента (~3%) согласуются с литературными данными. Что касается температуры перехода (основного и побочного пиков теплоемкости) и, особенно, энтальпии и энтропии перехода, совпадение величин с литературными данными удивительно хорошее (ΔtrН различаются на 0,05%, а ΔtrS совпадают).
Сделан вывод, что основной пик на кривой теплоемкости ферроцена можно отнести к фазовому переходу первого рода (Ttr = 163,9К), сопровождающемуся переходом триклинной кристаллической решетки в моноклинную. На него накладывается фазовый переход типа «порядок-беспорядок» (Тtr = 169К). Результатом наложения этих двух переходов и является сложная по форме аномалия кривой Сp = f(T) в области 125-200К (рис. 1).
Очень интересны работы, посвященные термодинамике ферроцена, японских исследователей Огасахара, Сораи и Суга. Изучая теплоемкость его в области 13-300К, они в случаях охлаждения ферроцена со скоростью, большей 1K в минуту, тоже обнаружили только один переход при 163,9К в пределах ошибок определения с теми же энтальпией и энтропией, что были определены ранее. Однако при охлаждении с меньшими скоростями был установлен тоже один, но другой, переход при 242К. При этом, как по термодинамическим результатам, так и методами рефракции рентгеновских лучей и нейтронов, а также по лазерным рамановским спектрам, не только для обычного ферроцена, но и для его дейтероаналога Fe(C5D5)2 было показано, что оба перехода являются фазовыми превращениями I рода.
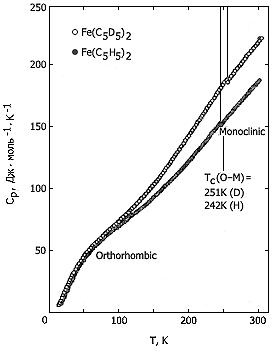
Рис. 1. Температурная зависимость теплоемкости
ферроцена и дейтероферроцена
На кривых температурной зависимости теплоемкости (рис. 1) виден верхний переход – при 242К у ферроцена и 251К – у дейтероферроцена. Это равновесный фазовый переход I рода из стабильной низкотемпературной орторомбической фазы в стабильную высокотемпературную моноклинную фазу. Энтальпия этого перехода 4,145 кДж·моль-1, энтропия 17,13 Дж·моль-1К-1 (у обычного ферроцена). На рис. 2, также по теплоемкости, показан нижний переход λ-типа. Это переход образующейся при охлаждении быстрее чем 1K в минуту метастабильной низкотемпературной триклинной фазы в метастабильную же переохлажденную высокотемпературную моноклинную фазу. Температура его 163,9К у Н- и 164,1К у D-ферроцена; энтальпия его 0,90 кДж·моль-1, энтропия – 5,5 Дж·моль-1К-1 (у Fe(C5H5)2). Ниже λ-перехода можно метастабильную низкотемпературную фазу перевести в стабильную низкотемпературную фазу (термообработка при 190К), причем при 156К выделяется 3,3 кДж·моль-1 энергии.
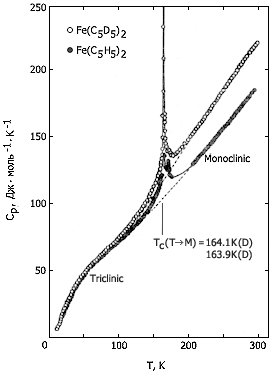
Рис. 2. Температурная зависимость теплоемкости метастабильных кристаллических форм ферроцена и дейтероферроцена
Далее японские исследователи рассчитали различие в нулевых энтальпиях стабильной и метастабильной низкотемпературных фаз (у метастабильной фазы нулевая энтальпия больше) и энтропию обеих фаз. При этом было положено, что нулевая энтропия стабильной фазы равна нулю, тогда расчет показал, что нулевая энтропия метастабильной низкотемпературной фазы, с учетом погрешности расчета, тоже равна нулю. Из этого следует, что и триклинная фаза является внутренне равновесной (упорядоченным кристаллом), но метастабильной относительно орторомбической.
Что же касается взаимной ориентации циклопентадиенильных колец в молекуле, то показано, что как ниже λ-перехода, так и выше его в обеих метастабильных фазах (низкотемпературной и высокотемпературной) имеет место одно и то же усредненное наложение молекул с различными ориентациями циклопентадиенильных колец.
Давление пара и термодинамические характеристики парообразования ферроцена изучены достаточно подробно. Измерения проводили как статическим, так и эффузионным методами, причем обоими методами получили хорошо совпадающие результаты. Очень близкие результаты получены с использованием эффузионного метода. Зависимость давления пара и энтальпии сублимации ферроцена от температуры в интервале 293-301К выражается уравнениями:
lgР = 30,29 - 4581/T - 6,04lgT
и
ΔsH(T) = (87,70 ± 0,54) - 0,050T.
Для термодинамических расчетов следует использовать, по-видимому, среднее значение Δs(298,15) = 73,04 ± 0,68 кДж·моль-1. Эти данные использованы для расчета стандартной энтропии ферроцена в газовом состоянии. Получено значение S°(298,15; г) = 365,3 ± 2,4 Дж·моль-1К-1. Рассчитаны также ΔfS° и ΔfG° (табл. 1).
Таблица 1
Энтропия и функция Гиббса образования дициклопентадиенилжелеза
-ΔfS°(298,15; к),
Дж·моль-1K-1 |
-ΔfS°(298,15; г),
Дж·моль-1K-1 |
-ΔfG°(298,15; к),
кДж·моль-1 |
-ΔfG°(298,15; г),
кДж·моль-1 |
| 520,8 ± 1,4 |
371,8 ± 2,6 |
310,1 ± 4,3 |
338,7 ± 4,4 |
Проведен расчет энтропии Fe(C5H5)2 в газовом состоянии с учетом новых спектральных данных. Получена величина S°(298,15; г) = 366,14 Дж·моль-1К-1. Чтобы определить величину потенциального барьера, тормозящего внутреннее вращение циклопентадиенильных колец в молекуле ферроцена, Vo, рассчитана также величина S°(298,15; г) по калориметрическим данным. Получено значение S°(298,15; г) = 365,7 ± 1,3 Дж·моль-1К-1, хорошо согласующееся с полученным значением. Поскольку значения энтропии, рассчитанные по калориметрическим и спектральным данным, совпадают в пределах ошибок их определения, нет заметного барьера вращения циклопентадиенильных колец в газовой фазе.
Проведен расчет термодинамических функций газообразного ферроцена в области 298,15-1000К. Результаты расчета приведены в таблице 2.
Таблица 2
Теплоемкость и термодинамические функции дициклопентадиенилжелеза в идеальном газовом состоянии
| T, K |
Cp,
Дж·моль-1·K-1 |
S°(T),
Дж·моль-1·K-1 |
[H°(T)–H°(298)]T-1,
Дж·моль-1K-1 |
-[G°(T)–H°(298)]T-1,
Дж·моль-1K-1 |
| 298,15 |
146,7 |
358,9 |
0 |
358,9 |
| 500 |
246,5 |
457,3 |
80,21 |
377,1 |
| 700 |
314,5 |
550,5 |
138,1 |
412,4 |
| 900 |
359,9 |
634,3 |
182,7 |
451,6 |
| 1000 |
377,2 |
672,7 |
201,3 |
471,4 |
Рассчитана стандартная энтропия газообразного ферроцена по калориметрическим данным и данным о давлении пара и энтальпии сублимации. Получено значение S°(298,15; г) = 363,1 ± 2,1 Дж·моль-1К-1. Рассчитана также S°(298,15; г) статистическим путем с учетом новых литературных данных о молекулярных постоянных ферроцена. Получено значение 360,0 ± 1,3 Дж·моль-1К-1, которое согласуется с калориметрическим значением в пределах ошибок определения обоих значений энтропии.
|